はじめに
こんにちは。巷ではDeep LearningやAIが流行りに流行っていると感じます。多くの企業・個人が何かしらの形で手を出しているのではないでしょうか。私も例に漏れずDeep Learning関連の技術検証を行っております。しかし、今回話すのは全く違う話です。単純な、データの確認の仕方の話です。グラフについて、しかも箱ひげ図のみをピックアップします。理由は、分析手法を選択する際にデータの確認は必須だと考えるからです。目的によっては、この時点で解決が見えるかもしれません。
箱ひげ図とは
箱ひげ図は五数要約(five-number summary)と呼ばれる(頑健な)要約統計量
Q0/4 : 最小値(minimum)
Q1/4 : 第1四分位点(lower quartile)
Q2/4 : 中央値(第2四分位点、median)
Q3/4 : 第3四分位点(upper quartile)
Q4/4 : 最大値(maximum)
を表すグラフである。第1四分位点から第3四分位点までの高さに箱を描き、中央値で仕切りを描く。
Wikipedia「箱ひげ図」 定義 より
です!!
~~とは、を説明するのにWikipedia以上のものは中々ないですね。ただ、文章だけでは図はイメージしづらいので、PythonとIrisデータセットを用いて実際に書いてみましょう。実行環境はGoogle Colaboratoryを用います。
import matplotlib.pyplot as pltfrom sklearn import datasetsimport pandas as pd%matplotlib inline# データの読み込みiris = datasets.load_iris()data = pd.DataFrame(iris.data)plt.boxplot(data.loc[:,0])data.loc[:,0].describe() # 基本統計量の確認 |
一目で五数要約が見られますね。注釈は画像を加工して入れています。中央にある四角を「箱」と、箱から伸びている線を「ひげ」と呼びます。ライブラリによってはひげが最大値・最小値でない場合があるため、注意が必要です。というかその方が多いです。その場合、上は「 (第3四分位点 – 第1四分位点) * 1.5 + 第3四分位点」と「最大値」の小さいほうが一般的です。その範囲から出たものは外れ値として扱うことで、図の印象が外れ値に引っ張られるのを避けることができます。
箱ひげ図からわかること
前項で使ったIrisデータセットを用いて簡単に説明しようと思います。IrisデータセットはMachine Learning Repositoryで提供されているデータセットです。アヤメの品種を、花弁とがくのデータから判別するという課題になります。このくらいのデータ数であれば正直色々な手法を試していけばうまくいくのですが、データ数が多くなってくるとある程度目星をつけた分析をしたいところです。そのため、まずデータ傾向を確認するときに箱ひげ図を用います。散布図とヒストグラムも個人的に見たいところですが、趣旨がぶれるため今回は割愛します。
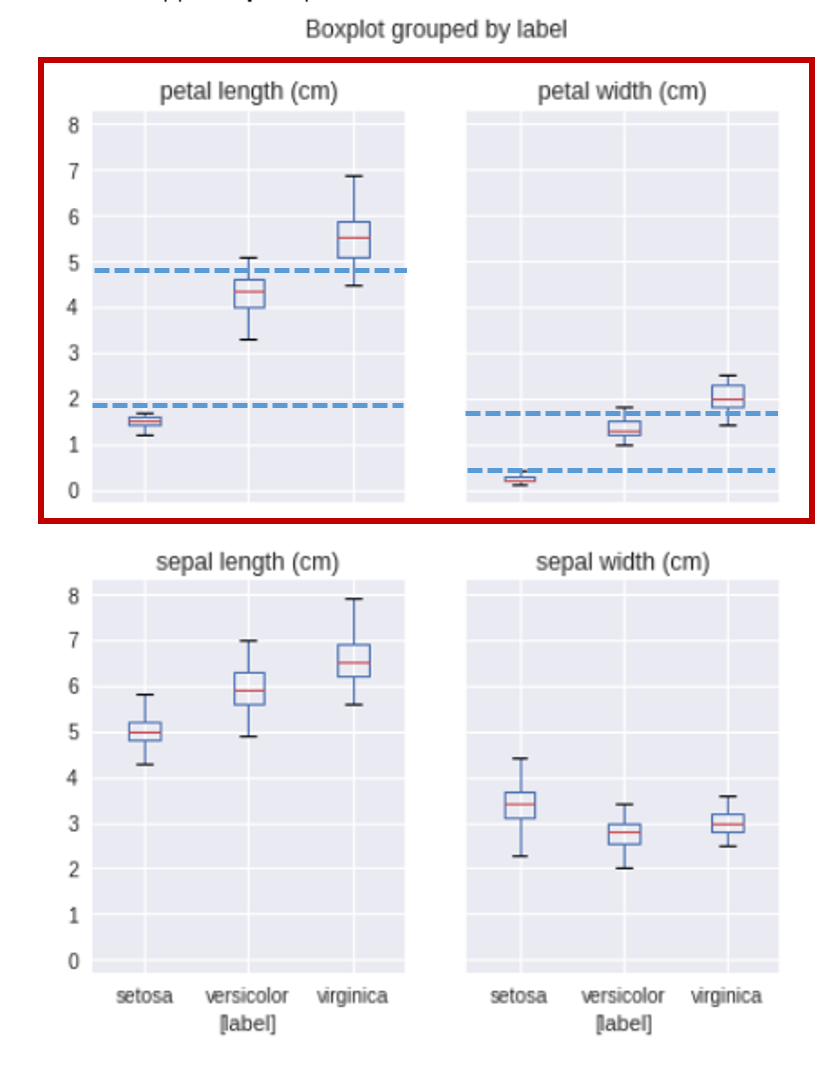
では指標ごとに箱ひげ図を描いてみましょう。
# データの準備data.columns = iris.feature # 列名定義data["label"] = iris.target_names[iris.target] # 品種列追加data.boxplot(by="label",layout=(4,1),figsize = (4,10)) # 描画 |
petal(花弁)の lengthと widthにおいて、箱が重なっていませんね。どうやらこの2指標に関しては、種類ごとにかなり差があるようです。分類できそうですね!また、2指標だけでもそこそこの結果は得られそうです。
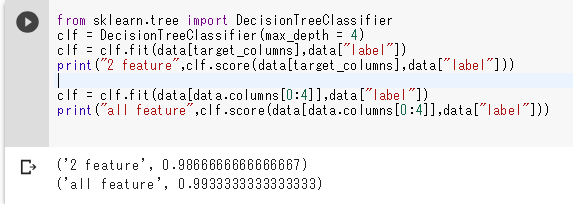
ということで、選択した2指標と全指標で決定木にかけてみます。比較が目的なのでトレーニングとテストのデータは分離しません。
print(data.columns) # 列名の確認# 使用する列の選択target_columns = data.columns[[2,3]]print(target_columns) |
結果:
Index([u’sepal length (cm)’, u’sepal width (cm)’, u’petal length (cm)’, u’petal width (cm)’, u’label’], dtype=’object’)
Index([u’petal length (cm)’, u’petal width (cm)’], dtype=’object’)
from sklearn.tree import DecisionTreeClassifier#決定木による分類機を定義clf = DecisionTreeClassifier(max_depth = 4) # シンプルなモデルにするため指標数分の深度# 2指標のみclf = clf.fit(data[target_columns],data["label"])print("2 feature",clf.score(data[target_columns],data["label"]))# 全指標clf = clf.fit(data[data.columns[0:4]],data["label"])print("all feature",clf.score(data[data.columns[0:4]],data["label"])) |
全て追加したほうが精度はいいですが、指標を倍にしたにもかかわらず0.7%ほどしか精度が上がっていません。2指標だけでもそこそこの結果は得られました!
実際に役に立つ状況
データの集計を行う際、分布や基本統計量を沢山見なくてはいけない段階があると思います。細かい確認にはもちろん数値等が必要ですが、おおざっぱな確認は箱ひげ図で事足りると思います。実際私も、箱ひげ図とイベントを重ねて表示することで、分析に用いる集計値の選択を行ったことがあります。混合ガウスモデルで分布推定して生起確率から外れ値を求め……など、選択してからも分析を行わなければなりませんが、簡単に指標を絞ることでより深い分析をすることができました。また、計算リソースと人的コストの節約にもなりました。
おわりに
いかがだったでしょうか。勉強段階で整ったデータセットのみを使っているとあまり触れない部分だったので改めてまとめてみましたが、恐らくとても当たり前の内容だったと思います。
他にも、軽い分布予想や外れ値閾の当たり付けなど、箱ひげ図でできることは色々あります。実務では色々な可視化・分析を試したほうがいい場合も多くありますが、箱ひげ図を掘り下げるだけでも楽しめます!また、散布図・ヒストグラム・ヴァイオリン図など他にも確認したい図はたくさんあります。
さらに、図を使った分析に慣れると報告資料に載せる図にも悩みづらくなります。是非お試しください!機会があったら散布図も紹介したいと思っております。
執筆者プロフィール

- tdi デジタルイノベーション技術部
-
入社して半年間ロボコン活動に専念。少しのJavaエンジニア期間を経てデータ分析や機械学習、Deep Learningをテーマに勤労しております。
昔取った杵柄を摩耗させつつ新たな支えを求めて試行錯誤中。
この執筆者の最新記事
 Pick UP!2020年10月30日Python/Kerasで学習させたモデルをJavaで動かすだけじゃ速くならなかった
Pick UP!2020年10月30日Python/Kerasで学習させたモデルをJavaで動かすだけじゃ速くならなかった ITコラム2020年8月4日DL4Jを使うためにEclipseでMaven使おうとして困ったら
ITコラム2020年8月4日DL4Jを使うためにEclipseでMaven使おうとして困ったら AI2019年11月29日AIの検証・開発を行うときに必要なハードウェア条件とは?
AI2019年11月29日AIの検証・開発を行うときに必要なハードウェア条件とは? AI2019年8月5日Google Colaboratoryの無料GPU環境を使ってみた
AI2019年8月5日Google Colaboratoryの無料GPU環境を使ってみた